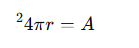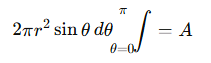من أين جاء قانون مساحة الكرة؟

عندما تتأمل في الكرة، ذلك الشكل المثالي الذي يعكس التناسق في أبهى صوره، قد تتساءل: من أين جاء قانون مساحة سطحها؟ هل وُجد هكذا دون تفسير؟ أم أن هناك رحلة رياضية معقدة تقف وراءه؟ الإجابة ليست فقط في الأرقام، بل في عبقرية عقول عبرت قرونًا من البحث حتى وصلت إلى الصيغة الساحرة:

لكن لماذا 4πr² بالضبط؟ لماذا ليس 5πr² أو أي عدد آخر؟ لنغوص في عمق هذا اللغز الرياضي ونفك شفرة هذا القانون.

البداية: نظرة تاريخية

قبل أن تأتي الرياضيات الحديثة بقوانينها المنهجية، كانت الهندسة تُدرس بأساليب تعتمد على الحدس والملاحظة. في العصور القديمة، حاول العلماء فهم العلاقات بين الأشكال ثلاثية الأبعاد، وبدأوا باستكشاف المجسمات الأساسية كالكرة والهرم والمخروط.

أرخميدس: العبقري الذي فك الشيفرة

العبقري اليوناني أرخميدس (287-212 ق.م) كان من أوائل من اكتشفوا العلاقة بين مساحة سطح الكرة ومساحة سطح الأسطوانة التي تحتويها. قام أرخميدس بحساب مساحة الكرة من خلال مقارنة حجمها مع حجم الأسطوانة، ووجد أن الكرة تشغل ثلثي حجم الأسطوانة المحيطة بها. لكن كيف قادته هذه الفكرة إلى القانون نفسه؟

الفكرة الجوهرية: التقطيع إلى شرائح لا نهائية

لنفترض أنك تريد حساب مساحة سطح الكرة، لكن كيف تفعل ذلك لمجسم منحني بالكامل؟ هنا يأتي الحل العبقري: التكامل.

1. تقسيم الكرة إلى شرائح دقيقة جدًا

إذا قسمنا سطح الكرة إلى عدد لا نهائي من الحلقات الصغيرة جدًا، فإن كل حلقة يمكن اعتبارها وكأنها سطح مستوٍ. هذه الفكرة هي جوهر التكامل، حيث نقوم بحساب مجموع مساحات هذه الحلقات اللامتناهية.

2. التكامل هو المفتاح

من خلال حساب المساحة باستخدام حساب التفاضل والتكامل، نحصل على الصيغة النهائية:

وهذا التكامل يؤدي في النهاية إلى النتيجة المذهلة:

لماذا 4π؟ سر التناسب مع الدائرة

من المثير للدهشة أن مساحة سطح الكرة ترتبط ارتباطًا وثيقًا بمساحة الدائرة. تذكر أن مساحة الدائرة هي πr²، لذا يمكننا أن نفكر في مساحة سطح الكرة على أنها 4 أضعاف مساحة دائرة كبيرة مرسومة داخلها.

لكن لماذا 4 تحديدًا؟ هذا الرقم ينبثق من العلاقة بين محيط الدائرة وزوايا الكرة. عندما يتم توزيع النقاط على سطح الكرة بشكل متساوٍ، فإن التكامل يأخذ في الحسبان جميع الاتجاهات، ما يؤدي إلى هذا العامل 4 المدهش.

العلاقة بين الحجم والمساحة: لمسة أخرى من العبقرية

هل لاحظت أن حجم الكرة يُعطى بالمعادلة:

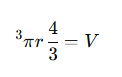
هذا ليس مجرد صدفة! عند اشتقاق حجم الكرة بالنسبة لنصف القطر r، نجد:

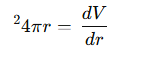
وهذا يعني أن معدل تغير حجم الكرة هو مساحة سطحها! هذا دليل رياضي مذهل على أن القانون ليس مجرد مصادفة، بل هو متجذر في أساسيات الهندسة الرياضية.

خاتمة: كيف غير هذا القانون وجه العلوم؟

لا يقتصر هذا القانون على الرياضيات البحتة، بل له تأثير عميق في الفيزياء والفلك. سواء كنت تدرس الكواكب، أو تريد فهم كيفية توزيع الحرارة على سطح جسم كروي، أو حتى تبحث في الظواهر الكمومية، فإن قانون مساحة الكرة هو أحد القوانين الأساسية التي لا غنى عنها.

وهكذا، لم تكن 4πr² مجرد صدفة أو تخمين، بل نتاج قرون من البحث، ونتيجة مباشرة لعبقرية العقول التي فككت تعقيدات الهندسة وحولت الأفكار إلى قوانين خالدة. السؤال الآن: هل هناك أسرار أخرى مخفية في الأشكال التي نراها كل يوم؟